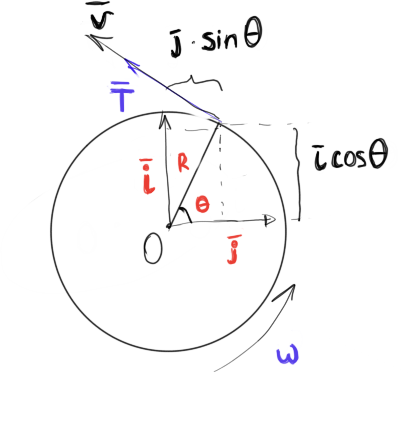
In the case of circular motion, the material point moves along the trajectory of a circle of constant radius R around the fixed center of rotation O
Radius is the vector of the position of a point on a circle:
R = R(t) =R * (i*cos(Ѳ) + j*sin(Ѳ))
The time derivatives for speed and acceleration will have the form:
V=dr/dt=dr/dѲ * dѲ/dt = R * dѲ/dt (-isin(Ѳ) + jcos(Ѳ))
According to the definition, the velocity shows the change in the position of a point on the trajectory s during time t, in this case, the trajectory depends on the angle of movement and the radius of the circle:
s = rѲ
where s is the path traveled along the trajectory, R is the radius of the circle (constant), Ѳ is the angle of rotation
V=|V|=ds/dt=R * dѲ/dt = R ω
ω is the angular velocity, has dimension T-1 , in the si system rad/s, in everyday use degree/s, revolution/s, revolution/min
The velocity vector is directed along the tangent circle, i.e.:
V = R ω T
where T is the unit vector of the tangent.
Angular acceleration is usually denoted by the symbol α. Angular acceleration is the derivative of angular velocity in time or the second derivative of angle in time:
α = dω/dt = d2Ѳ/dt2

