Electronic configuration of the atom
The electronic configuration of an atom is a formula showing the arrangement of electrons in an atom by levels and sublevels. After studying the article, you will learn where and how electrons are located, get acquainted with quantum numbers and you will be able to build an electronic configuration of an atom by its number, at the end of the article there is a table of elements.
Why study the electronic configuration of elements?
Atoms as a constructor: there are a certain number of details, they differ from each other, but two details the same type are exactly the same. But this constructor is much more interesting than a plastic one and that's why. The configuration changes depending on who is nearby. For example, oxygen next to hydrogen can it turns into water, next to sodium into gas, and being next to iron turns it into rust at all. To answer the question of why this happens and to predict the behavior of an atom next to another is necessary to study the electronic configuration, which will be discussed below.
How many electrons are there in an atom?
An atom consists of a nucleus and electrons rotating around it, a nucleus consists of protons and neutrons. In neutral in the state of each atom, the number of electrons is equal to the number of protons in its nucleus. Quantity protons are designated by the ordinal number of the element, for example, sulfur has 16 protons - the 16th element of the periodic table the system. Gold has 79 protons - the 79th element of the periodic table. Accordingly, in sulfur in neutral there are 16 electrons in the state, and 79 electrons in gold.
Where to look for an electron?
Observing the behavior of the electron, certain patterns were deduced, they are described quantum numbers, there are four of them in total:
- The main quantum number
- Orbital quantum number
- Magnetic quantum number
- Spin quantum number
Orbital
Next, instead of the word orbit, we will use the term "orbital", the orbital is the wave function of an electron, roughly, this is the area where the electron spends 90% of the time.
N - level
L - shell
Ml - orbital number
Ms - the first or second electron in the orbital
Orbital quantum number l
As a result of the study of the electron cloud, we found that depending on the energy level, the cloud takes four main forms: a ball, dumbbells and the other two, more complex. In order of increasing energy, these forms are called s-, p-, d- and f-shells. On each of these shells there can be 1 (on s), 3 (on p), 5 (on d) and 7 (on f) orbitals. The orbital quantum number is the shell on which the orbitals. The orbital quantum number for s,p,d and f-orbitals, respectively , takes the values 0,1,2 or 3.
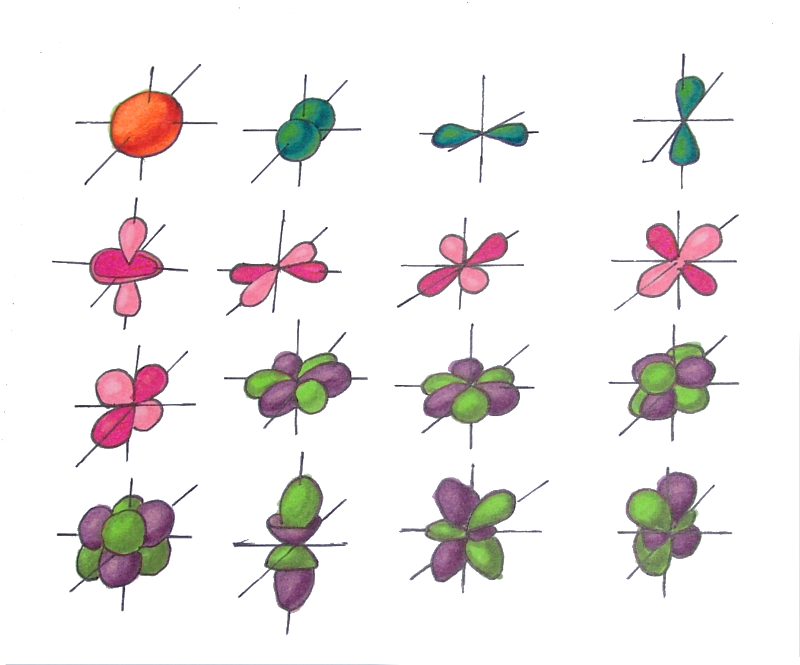
There is one orbital on the s-shell (L=0) - two electrons
There are three orbitals on the p-shell (L=1) - six electrons
There are five orbitals on the d-shell (L=2) - ten electrons
There are seven orbitals on the f-shell (L=3) - fourteen electrons
Magnetic quantum number ml
There are three orbitals on the p-shell, they are denoted by numbers from -L to +L, that is, for the p-shell (L=1) there are orbitals "-1", "0" and "1". The magnetic quantum number is denoted by the letter ml.
It 's easier for electrons inside the shell they are located in different orbitals, so the first electrons fill one for each the orbital, and then each is joined by its pair.
Consider the d-shell:
the d-shell corresponds to the value L=2, that is, five orbitals (-2,-1,0,1 and 2), the first five electrons fill the shell taking the values Ml=-2,Ml=-1,Ml=0, Ml=1,Ml=2.
Spin quantum number ms
Spin is the direction of rotation of an electron around its axis, there are two directions, so the spin quantum number it has two values: +1/2 and -1/2. There can be two electrons on the same energy sublevel only with opposite backs. The spin quantum number is denoted by ms
The main quantum number n
The main quantum number is the energy level, at the moment seven energy levels are known, each is denoted by an Arabic numeral: 1,2,3,...7. The number of shells at each level is equal to the level number: on the first level there is one shell, on the second two, etc.
Electron number

So, any electron can be described by four quantum numbers, the combination of these numbers is unique for each electron positions, take the first electron, the lowest energy level is N=1, at the first level there is one shell, the first shell at any level has the shape of a ball (s-shell), i.e. L=0, a magnetic quantum number can take only one value, Ml=0 and the spin will be +1/2. If we take the fifth electron (in whatever atom it is), then the main quantum numbers for it will be: N=2, L=1, M= -1, spin 1/2.
Energy levels with sublevels are shown below for clarity, the levels are located from top to bottom and the sublevels are separated by color:
| 1 | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | |||||||||||||||||||
| 3 | |||||||||||||||||||
| 4 | |||||||||||||||||||
| 5 | |||||||||||||||||||
| 6 | |||||||||||||||||||
| 7 | |||||||||||||||||||
| 8 | |||||||||||||||||||
| Table 1. Electron distribution by energy levels | |||||||||||||||||||
Here, the energy levels (1-7) are shown from top to bottom, from left to right they are divided into groups. sublevels (s,p,d, f), in each cell there are two electrons in opposite directions. General the principle of electron distribution is such that the energy sublevels are filled in the order of the sum of the main and the orbital quantum numbers, that is: 1S, 2S, 2P, 3S, 3P, 4S, 3D and so on, if the sum is the same, then first , the level with the smaller main quantum number N is filled in.
Some elements have deviations in the formation of the electronic configuration, namely 24Cr, 29Cu, 41Nb, 42Mo, 44Ru, 45Rh, 46Pd, 47Ag, 78Pt, 79Au
Elements
Check yourself, make an electronic configuration for the elements #5, #14and #22, then check yourself in the table below.
| № |
| |||
|---|---|---|---|---|
| 1 | H | 1s 1 | 1 | |
| 2 | He | 1s 2 | 1 | |
| 3 | Li | 1s 22s 1 | 2 | |
| 4 | Be | berillii | 1s 22s 2 | 2 |
| 5 | B | 1s 22s 22p 1 | 2 | |
| 6 | C | 1s 22s 22p 2 | 2 | |
| 7 | N | 1s 22s 22p 3 | 2 | |
| 8 | O | 1s 22s 22p 4 | 2 | |
| 9 | F | 1s 22s 22p 5 | 2 | |
| 10 | Ne | nothe | 1s 22s 22p 6 | 2 |
| 11 | Na | 1s 22s 22p 63s 1 | 3 | |
| 12 | Mg | 1s 22s 22p 63s 2 | 3 | |
| 13 | Al | 1s 22s 22p 63s 23p1 | 3 | |
| 14 | Si | 1s 22s 22p 63s 23p2 | 3 | |
| 15 | P | 1s 22s 22p 63s 23p3 | 3 | |
| 16 | S | 1s 22s 22p 63s 23p4 | 3 | |
| 17 | Cl | 1s 22s 22p 63s 23p5 | 3 | |
| 18 | Ar | 1s 22s 22p 63s 23p6 | 3 | |
| 19 | K | 1s 22s 22p 63s 23p64s 1 | 4 | |
| 20 | Ca | kalbcii | 1s 22s 22p 63s 23p64s 2 | 4 |
| 21 | Sc | 1s 22s 22p 63s 23p64s 23d1 | 4 | |
| 22 | Ti | titAn | 1s 22s 22p 63s 23p64s 23d2 | 4 |
| 23 | V | 1s 22s 22p 63s 23p64s 23d3 | 4 | |
| 24 | Cr | hrom | 1s 22s 22p 63s 23p64s 13d5 | 4 |
| 25 | Mn | 1s 22s 22p 63s 23p64s 23d5 | 4 | |
| 26 | Fe | wateezoh | 1s 22s 22p 63s 23p64s 23d6 | 4 |
| 27 | Co | 1s 22s 22p 63s 23p64s 23d7 | 4 | |
| 28 | Ni | hikateb | 1s 22s 22p 63s 23p64s 23d8 | 4 |
| 29 | Cu | 1s 22s 22p 63s 23p64s 13d10 | 4 | |
| 30 | Zn | 1s 22s 22p 63s 23p64s 23d10 | 4 | |
| 31 | Ga | 1s 22s 22p 63s 23p64s 23d104p1 | 4 | |
| 32 | Ge | 1s 22s 22p 63s 23p64s 23d104p2 | 4 | |
| 33 | As | 1s 22s 22p 63s 23p64s 23d104p3 | 4 | |
| 34 | Se | 1s 22s 22p 63s 23p64s 23d104p4 | 4 | |
| 35 | Br | 1s 22s 22p 63s 23p64s 23d104p5 | 4 | |
| 36 | Kr | 1s 22s 22p 63s 23p64s 23d104p6 | 4 | |
| 37 | Rb | 1s 22s 22p 63s 23p64s 23d104p65s1 | 5 | |
| 38 | Sr | 1s 22s 22p 63s 23p64s 23d104p65s2 | 5 | |
| 39 | Y | 1s 22s 22p 63s 23p64s 23d104p65s24d1 | 5 | |
| 40 | Zr | 1s 22s 22p 63s 23p64s 23d104p65s24d2 | 5 | |
| 41 | Nb | 1s 22s 22p 63s 23p64s 23d104p65s14d4 | 5 | |
| 42 | Mo | 1s 22s 22p 63s 23p64s 23d104p65s14d5 | 5 | |
| 43 | Tc | 1s 22s 22p 63s 23p64s 23d104p65s24d5 | 5 | |
| 44 | Ru | 1s 22s 22p 63s 23p64s 23d104p65s14d7 | 5 | |
| 45 | Rh | 1s 22s 22p 63s 23p64s 23d104p65s14d8 | 5 | |
| 46 | Pd | 1s 22s 22p 63s 23p64s 23d104p64d10 | 5 | |
| 47 | Ag | cerfuckro | 1s 22s 22p 63s 23p64s 23d104p65s14d10 | 5 |
| 48 | Cd | 1s 22s 22p 63s 23p64s 23d104p65s24d10 | 5 | |
| 49 | In | andndii | 1s 22s 22p 63s 23p64s 23d104p65s24d105p1 | 5 |
| 50 | Sn | 1s 22s 22p 63s 23p64s 23d104p65s24d105p2 | 5 | |
| 51 | Sb | surma | 1s 22s 22p 63s 23p64s 23d104p65s24d105p3 | 5 |
| 52 | Te | 1s 22s 22p 63s 23p64s 23d104p65s24d105p4 | 5 | |
| 53 | I | yod | 1s 22s 22p 63s 23p64s 23d104p65s24d105p5 | 5 |
| 54 | Xe | 1s 22s 22p 63s 23p64s 23d104p65s24d105p6 | 5 | |
| 55 | Cs | tsezeeth | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s1 | 6 |
| 56 | Ba | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s2 | 6 | |
| 57 | La | lAnthatn | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s25d1 | 6 |
| 58 | Ce | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f2 | 6 | |
| 59 | Pr | nRazeodthem | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f3 | 6 |
| 60 | Nd | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f4 | 6 | |
| 61 | Pm | nrometith | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f5 | 6 |
| 62 | Sm | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f6 | 6 | |
| 63 | Eu | ebpopii | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f7 | 6 |
| 64 | Gd | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f75d1 | 6 | |
| 65 | Tb | terbith | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f9 | 6 |
| 66 | Dy | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f10 | 6 | |
| 67 | Ho | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f11 | 6 | |
| 68 | Er | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f12 | 6 | |
| 68 | Tm | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f13 | 6 | |
| 70 | Yb | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f14 | 6 | |
| 71 | Lu | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d1 | 6 | |
| 72 | Hf | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d2 | 6 | |
| 73 | Ta | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d3 | 6 | |
| 74 | W | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d4 | 6 | |
| 75 | Re | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d5 | 6 | |
| 76 | Os | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d6 | 6 | |
| 77 | Ir | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d7 | 6 | |
| 78 | Pt | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s14f145d9 | 6 | |
| 79 | Au | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s14f145d10 | 6 | |
| 80 | Hg | rtutb | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d10 | 6 |
| 81 | Tl | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p1 | 6 | |
| 82 | Pb | cveenotc | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p2 | 6 |
| 83 | Bi | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p3 | 6 | |
| 84 | Po | byloneitherth | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p4 | 6 |
| 85 | At | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p5 | 6 | |
| 86 | Rn | phellhe | 1s 22s 22p 63s 23p64s 23d104p65s14d105p66s24f145d106p6 | 6 |
| 87 | Fr | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s1 | 7 | |
| 88 | Ra | phellii | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s2 | 7 |
| 89 | Ac | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s26d1 | 7 | |
| 90 | Th | tyellii | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s26d25f0 | 7 |
| 91 | Pa | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f26d1 | 7 | |
| 92 | U | yRan | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f36d1 | 7 |
| 93 | Np | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f46d1 | 7 | |
| 94 | Pu | plutheii | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f56d1 | 7 |
| 95 | Am | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f7 | 7 | |
| 96 | Cm | kyurith | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f76d1 | 7 |
| 97 | Bk | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f86d1 | 7 | |
| 98 | Cf | kalifyellneitherth | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f10 | 7 |
| 99 | Es | eynpcherneitherth | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f11 | 7 |
| 100 | Fm | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f12 | 7 | |
| 101 | Md | mendateherveeth | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f13 | 7 |
| 102 | No | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f14 | 7 | |
| 103 | Lr | lourensith | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d1 | 7 |
| 104 | Rf | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d2 | 7 | |
| 105 | Db | dubny | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d3 | 7 |
| 106 | Sg | siborgiy | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d4 | 7 |
| 107 | Bh | bori | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d5 | 7 |
| 108 | Hs | hassiy | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d6 | 7 |
| 109 | Mt | meitnerium | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d7 | 7 |
| 110 | Ds | darmstadt | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d8 | 7 |
| 111 | Rg | x-ray | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d9 | 7 |
| 112 | Cn | copernicus | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d10 | 7 |
| 113 | Nh | nihonium | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d107p1 | 7 |
| 114 | Fl | flerovium | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d107p2 | 7 |
| 115 | Mc | muscovy | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d107p3 | 7 |
| 116 | Lv | livermore | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d107p4 | 7 |
| 117 | Ts | tennessee | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d107p5 | 7 |
| 118 | Og | oganeson | 1s 22s 22p 63s 23p64s 23d104p65s24d105p66s24f145d106p67s25f146d107p6 | 7 |
| Table 2. Electronic configuration of atoms | ||||
If you want to learn how to make an electronic configuration, refer to the article «how to write an electronic configuration»
Quantum numbers of electrons in atoms
